Učební úlohy jako „jádro výukové situace“ zasazené do různých sociálních, geografických, historických, uměleckých nebo technických kontextů, vyzývají žáka k řešení určitého problému, které by vedlo k jeho učení, k rozvoji jeho kompetencí a motivovalo jej k poznávání (Janík et al., 2013, s. 377). Motivaci zvyšuje „kontextualizace učební činnosti“ (Kalhous, & Obst et al., 2002, s. 368): když učitel volí učivo (učební úlohy a další aktivity) tak, aby odpovídalo žákovým potřebám a zájmům nebo ukazuje spojení učiva s reálným světem.
Fuchs a Zelendová (2015, s. 15) používají pro označení některých slovních (kontextových) úloh, které čerpají námět z různých oblastí životní reality, označení autentické slovní úlohy. Považují za ně takové, které se vyznačují určitými vlastnostmi: týkají se událostí, které by se mohly stát v běžném životě; obsahují otázky, které by mohly v běžném životě zaznít; žákům musí být jasný účel jejich řešení; jsou jednoduše a srozumitelně formulované; údaje potřebné k řešení úloh musejí být řešiteli k dispozici nebo snadno dohledatelné; musejí se týkat určité konkrétní události.
Vondrová, Rendl et al. (2015, s. 33) uvádějí výsledky výzkumu Palma (2008) se žáky 5. ročníku, v němž byly použity „autentické slovní úlohy“ oproti běžným slovním úlohám. Bylo zjištěno, že u autentičtějších úloh se významně zvýšila tendence žáků využít pro jejich řešení znalosti a zkušenosti z reálného života.
Při formulování autentických slovních úloh lze s výhodou využit aktuálních textů různých typů, které jsou svým obsahem blízké dnešní populaci, jsou pro žáky zajímavé, přinášejí konkrétní „příběh“. Jejich zdrojem se mohou stát tištěná i elektronická média. Je zřejmé, že využití médií nabývá stále většího významu. Musíme s nimi ve vzdělávání počítat jako s významným faktorem a nemůžeme je přehlížet nebo podceňovat. Zejména elektronická média, počítač, tablet, mobilní telefon, se stávají součástí života dnešního dítěte se všemi průvodními jevy. Multimediální encyklopedie a datové servery v prostředí internetu přebírají roli informačního a komunikačního média, slouží jako zdroj dat a informací nejrůznějšího charakteru. V současné situaci se zdá hledání způsobů, jak posilovat pozitivní působení digitálních médií a oslabovat jejich negativní vlivy, přínosnější než jejich démonizace. O významu uvedené problematiky svědčí také místo mediální výchovy v inovovaném kurikulu, v rámcových vzdělávacích programech. Přitom je zcela zřejmá souvislost mediální gramotnosti s rozvojem čtenářské gramotnosti žáků. Pozornost rozvíjení různých aspektů mediální a čtenářské gramotnosti si vyžaduje nejen školská praxe, ale především příprava žáků pro plnohodnotný život v informační společnosti.
Právě využití poznatků z okolního světa zprostředkovaného médii je prostředkem vnitřní motivace, poskytuje k ní zvláště vhodnou příležitost. Řešení autentických úloh převzatých z médií předpokládá a vyžaduje porozumění textu, usuzování z přečteného, a tím rozvíjení čtenářské gramotnosti.
Úlohy inspirované internetovým médiem
Zaměřím se na tvorbu autentických úloh z výchozího textu a jejich stručné metodické rozpracování pro konkrétní praxi výuky. Inspiraci poskytla spolupráce na realizaci projektu E. Fuchse a E. Zelendové Matematika v médiích, který byl realizován Národní ústavem pro vzdělávání ve spolupráci se Společností učitelů matematiky JČMF. Cílem projektu bylo nabídnout edukační praxi cestu, která by umožnila rozvíjet čtenářskou a matematickou gramotnost „ruku v ruce“ prostřednictvím tvorby a řešení úloh na konkrétní témata zveřejněná v médiích. Jako výstup řešení projektu byl zpracován metodický materiál s názvem Matematika v médiích. Využití slovních úloh při kooperativní výuce na základních a středních školách. (Fuchs, & Zelendová et al., 2015). Tým učitelek ze ZŠ v Tanvaldu Jana Duňková, Blanka Blažková a Zdeňka Jónová pod vedením Evy Novákové z Pedagogické fakulty MU v Brně do tohoto textu zařadil osm konkrétních rozpracovaných ukázek využití médií ve výuce matematiky na 1. stupni základní školy. Vyskytují se zde náměty s podtextem přírodopisným, historickým nebo zeměpisným. Žákům jsou poskytovány vstupní informace jiného předmětu, přičemž řešení učebních úloh je založeno na uplatnění matematických znalostí a dovedností žáků.
V článku uvádím další námět, jak mohou žáci na vhodně zvolených situacích a úlohách z reality objevovat vzájemné souvislosti z různých oborů a přitom aplikovat osvojené matematické znalosti. Pro zasazení do souboru úloh bylo třeba pečlivě zvážit délku textu a jeho zajímavost vzhledem k cílové žákovské skupině. Téma umožnilo významně uplatnit mezipředmětové vztahy matematiky a vlastivědy a matematiky a přírodovědy. Současně rozvíjí regionální problematiku.
Protržená přehrada Bílá Desná
Ukázka je inspirována internetovou stránkou www.ceskehory.cz. Z ní je převzata informace o tragické události, ke které došlo před více než sto lety v tehdejších Sudetech. Má nesporný motivační potenciál vzhledem k aktuálním zkušenostem z povodní, často se opakujícím záplavám a obecně ke klimatickým změnám.
Protržená přehrada na Bílé Desné byla prohlášena za kulturní památku v roce 1996. Stalo se tak k 80. výročí protržení přehrady. Byla budovaná od října 1912 do listopadu 1915, takže od dokončení až po její protržení uplynulo pouhých deset měsíců. Zaplavila obec Desnou. V obci zahynulo 62 lidí, 33 domů zničila voda zcela a 69 bylo vážně poškozeno. V Desné je umístěn pamětní kámen, který tehdy přivalila voda. Protržená hráz se šoupátkovou věží dosud stojí. V podzemní štole do sousedního údolí, v současnosti uzavřené, je významné zimoviště netopýrů. Dosud zde bylo zjištěno 11 druhů. Tato katastrofa na dlouhou dobu zastavila stavbu sypaných hrází ve světě. Přehrada nebyla nikdy obnovena a její trosky jsou dodnes mlčenlivým svědkem této tragédie. Nyní je na místě bývalé přehrady vyznačena krátká naučná stezka s několika zastávkami.
Zdroj: http://protrzena-prehrada-bila-desna.ceskehory.cz/.
Nyní následuje zadání úloh, jejich obsahová a formální charakteristika
Přehrada se začala budovat v roce …………na řece ……………………, která se nachází v dnešním Libereckém kraji. Najdeš ji v …………………………horách, poblíž měst ……. a……. V zaplavené obci bylo zcela zničeno nebo vážně poškozeno celkem ……………domů.
Zakresli přehradu do „slepé mapy“ ČR.
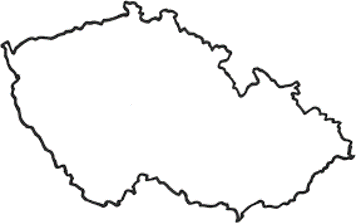
Geografické údaje, potřebné k řešení úlohy, je třeba vyhledat v informačních zdrojích, například zadat do vyhledávače heslo „Desná“, resp. „Bílá Desná“ a najít na mapě Liberecký kraj, Jizerské hory a města Liberec a Jablonec n. N.
Vyznač na vhodně zvolené časové přímce: ve kterém roce byla zahájena stavba přehrady, ve kterém byla dokončena, ve kterém roce došlo k jejímu protržení.
Odpovědi na otázky jsou jen zdánlivě snadné, vyžadují logický úsudek, dovednost analyzovat časová období s dobrou orientací v kalendáři, ale i použití početních operací zpaměti nebo písemně k potřebným výpočtům. Zadání vytváří prostor pro diskusi, argumentaci žáků, rozvíjení úvah o reálnosti údajů, např. kolik dní bylo skutečně pracovních aj.
Správná odpověď závisí na datu, kdy byla úloha řešena. V době naší pilotáže, v roce 2019, uplynulo 23 let od vyhlášení za kulturní památku, 107 let od zahájení výstavby a 104 let od dokončení.
První tři úlohy obsahují tvrzení, ve kterém musí žák doplnit čísla nebo slova na základě pozorného čtení úvodní ukázky. Jsou považovány za otevřené úlohy se stručnou odpovědí. Vyžadují, aby žák zformuloval a napsal vlastní odpověď (číslo, slovo, krátkou větu, vzorec apod.) – nevybírá z nabídnutých odpovědí, ale sám odpověď, řešení úlohy, produkuje (Chráska, 2007, s. 189).
Rozhodni o pravdivosti tvrzení na základě informací, které zjistíš na internetu.
Řešení úlohy vyžaduje přírodovědné znalosti. Předpokládá, že žák, který jimi pravděpodobně nedisponuje, dokáže vyhledat potřebné informace v internetovém vyhledávači (případně v tištěné literatuře – učebnici, encyklopedii apod.), a tím prokáže potřebnou míru čtenářské a informační gramotnosti.
Tato uzavřená úloha má podobu dichotomické volby mezi pravdivou a nepravdivou odpovědí. Jak uvádí Chráska (2007, s. 190), mezi nevýhody tohoto typu úloh patří nebezpečí „náhodného uhádnutí“ – jsou-li v nabídce dvě možné odpovědi, z nichž jedna je správná, je pravděpodobnost uhádnutí správné odpovědi 50 %. Odpověď neumožňuje odhalit aktivní znalost testovaného jevu, pouze jeho znovupoznání – žák by správnou odpověď nevyprodukoval, ale v nabídce odpovědí ji rozezná. Je tedy třeba nabídku odpovědí chápat jako pomoc při řešení úlohy.
Rovněž v této úloze jde o bezprostřední práci s úvodním textem. K řešení je třeba vypsat všechny čísla zapsaná číslicemi, ale také slovem – číslovka „deset“, a dále uplatnit základní aritmetické znalosti: vzestupné uspořádání přirozených čísel, rozlišení sudého a lichého čísla, znalost dekadické číselné soustavy (jednotky, desítky, dvojciferné číslo), operace sčítání a násobení. Vlastní numerické výpočty nejsou obtížné, vyžadují pouze znalost sčítání a násobení přirozených čísel zpaměti nebo písemně (případně s využitím kalkulátoru).
Slovní úloha, jejíž řešení vyžaduje informační gramotnost – vyhledávání a zpracování potřebných informací pomocí internetu.
Tvorba či obměna úloh bývá považována za aktivitu vysoké náročnosti. Žáci se při samostatné formulaci úlohy dostávají do nové role, kdy se z pasivního příjemce úloh zadaných učitelem nebo učebnicí stávají jejich samostatnými tvůrci, a blíží se tak samotné podstatě matematické aktivity. Pokusy žáků vedly k rozmanitým výsledkům, někdy spíše k formulaci otázek vycházejících nejen z výchozího textu, ale i zadaných úloh. Vytvořit smysluplné zadání slovní úlohy, obsahující podmínky potřebné k řešení a vhodně formulovanou otázku, se ukázalo jako velmi obtížné. Podle našeho názoru odráží uvedená skutečnost také to, že žáci nejsou na podobnou aktivitu zvyklí.
Závěrem
Příspěvek je zaměřen na tvorbu a následnou analýzu učebních úloh jako jednu z aktivit, jimiž lze významně obohatit výuku matematiky; jako na jednu z cest, jak vyvolat u učitelů i žáků potřebu dosáhnout hlubšího porozumění a prohloubit vlastní znalosti (Tichá & Hošpesová, 2011, s. 42). Soubor úloh byl volen tak, aby dokumentoval vzájemné propojení matematické, čtenářské a informační gramotnosti žáků jako podmínky a předpokladu úspěšného řešení. Úlohy k jednotlivým aktivitám byly vytvořeny tak, aby byly pro žáky podnětné, zajímavé a umožnily samostatnou práci. Ověřili jsme je v reálném prostředí matematické výuky v 5. ročníku ZŠ v rámci pilotáže projektu. Při pilotáži měli žáci k dispozici tablet/přístup k internetu, vyhledáním dat nezbytných k řešení úloh prokazovali potřebnou úroveň informační gramotnosti. Ukázalo se jako vhodné úlohy žákům prezentovat na pracovním listu, po doplnění údajů řešení úloh společně analyzovat. Aktivitu obsahující sedm úloh lze zařadit do jedné výukové hodiny. V souboru se vyskytují také úlohy, pro jejichž řešení musí žáci některé údaje dohledat. Vytváří se tím prostor pro realizaci aktivit, jež mohou přesáhnout časový horizont jedné výukové hodiny a umožňují samostatnou domácí přípravu s oporou o internetové zdroje. V tomto případě šlo o rozvíjení mediální gramotnosti ve smyslu využití potenciálu médií jako zdroje informací, nezbytných pro řešení úloh, resp. pro vyhledání správných odpovědí na otázky. Žáci museli uplatnit schopnost analyzovat nabízená sdělení, způsobilost zpracovat, vyhodnotit získané informace, a tím je využít k řešení úloh. Řešení úloh vyžaduje nenásilné seznámení žáků s fakty z různých oblastí lidské činnosti populární formou. Předpokládá aktivní přístup, umožňuje kooperativní učení, vytváří prostor pro samostatné objevování, dohledání potřebných údajů v dalších médiích a v jiných informačních zdrojích. Řešení úloh rozvíjí a obohacuje mezipředmětové vztahy matematiky s tematickými oblastmi Člověk a společnost, Člověk a příroda Rámcového vzdělávacího programu pro základní vzdělávání. Mají ale také značný motivační potenciál. Ten spočívá především v možnosti zaměřit se na poznávání nových míst, cestování, seznamování se s novými, neznámými objekty.
Uvedený soubor matematických úloh byl koncipován se snahou využít úvodního textu tak, aby úlohy nebyly monotónní, aby vyvolávaly celou škálu aktivit. Úlohy jsou uvozeny tzv. akčním slovem dvojího typu, které se stává podnětem pro realizaci následných činností žáků (Kalhous & Obst et al., 2002, s. 333) – buď slovesem v rozkazovacím způsobu (vyhledej v textu, vypiš, doplň), nebo tázací částicí. Rozmanitá je rovněž kognitivní obtížnost úloh[1]. Od úloh vyžadující uplatnění znalostí žáků, jejich reprodukci (numerické výpočty – vypočítej; sečti; vynásob), přes úlohy vyžadující myšlenkové operace s poznatky (rozhodni o pravdivosti; uspořádej), až po úlohy vyžadující sdělení poznatků (vysvětli, co znamená; vyhledej na mapě) a tvořivé myšlení (vytvoř úlohu).
Ze zkušeností, které jsme v našem týmu získaly, vyplývá, že texty z médií byly žáky přijaty velmi příznivě. Kladně hodnotily práci i zapojené paní učitelky. Tento způsob práce byl pro ně výzvou, jak prohloubit obsah matematického vzdělávání žáků skrze mediální text. V našem příkladu byl rovněž propojen dramatický příběh s mezipředmětovými vztahy a regionální tematikou. Samotná realizace byla impulzem pro další, navazující aktivity například v podobě výletu za netopýry k protržené přehradě, což se ukázalo jako zvláště působivé. Věřím, že toto téma může oslovit žáky napříč jednotlivými kraji, ale zároveň může být inspirací pro vytvoření vlastního souboru aktivit vycházejících ze zájmu vašich žáků, navazujících na váš region.
Literatura
Fuchs, M., & Zelendová, E. (Eds.). (2015). Matematika v médiích. Využití slovních úloh při kooperativní výuce na základních a středních školách. Praha: JČMF.
Chráska, M. (2007). Metody pedagogického výzkumu: základy kvantitativního výzkumu. Praha: Grada Publishing.
Janík, T. et al. (2013). Kvalita (ve) vzdělávání. Obsahově zaměřený přístup ke zkoumání a zlepšování kvality výuky. Brno: Masarykova univerzita.
Kalhous, Z., & Obst. O. et al. (2002). Školní didaktika. Praha: Portál.
Palm, T. (2008). Impact of authenticity on sense making in word problem solving. Educational Studies in Mathematics 67(1), 37–58.
Tichá, M., & Hošpesová, A. (2011). Gramotnost učitele matematiky a tvoření úloh. In A. Hošpesová, (Ed.) Matematická gramotnost a vyučování matematice. České Budějovice: Jihočeská univerzita.
Vondrová, N., & Rendl, M., et al. (2015). Kritická místa matematiky základní školy v řešeních žáků. Praha: Karolinum.
Mgr. Eva Nováková, Ph.D. je absolventka oboru Učitelství pro 1. stupeň základní školy a oboru Učitelství matematiky pro 2. stupeň základní školy na Pedagogické fakultě UP v Olomouci. Na Univerzitě Palackého absolvovala v roce 2005 doktorské studium v oboru Pedagogika. Učila pět let na základních školách v Přerově a v Brně. Je odbornou asistentkou katedry matematiky Pedagogické fakulty MU v Brně. Její odborné zaměření je orientováno na problematiku matematické pregramotnosti v mateřské škole a matematického vzdělávání v primární škole. Je autorkou řady publikací a příspěvků na odborných konferencích.
Kontakt: novakova@ped.muni.cz
[1] Podrobněji v publikaci Kalhouse, Obsta a kol. (2002). Školní didaktika. Praha: Portál, s. 328‒336.
Zvládání chování žáků se z mezinárodních výzkumů dlouhodobě ukazuje jako jedna z nejnáročnějších činností v rámci výuky jak pro studenty učitelství, tak pro začínající i pokročilé učitele (Paramita, Anderson & Sharma, 2020; OECD, 2019). Výzkum v České republice potvrdil, že přes 50 % začínajících učitelů považuje zvládání chování žáků za oblast, kde by potřebovali největší podporu (Juhaňák a kol., 2018).
(Vyšlo v časopise Komenský 148/1)
Článek pojednává o iniciativě, kterou zaměřujeme na podporu absolventů Pedagogické fakulty UK v jejich adaptační fázi pedagogické kariéry.
(Vyšlo v časopise Komenský 148/1)